Practical Dynamic Analysis and Design for Engineers and Architects

Sam Kassegne, PhD, PE

Course Outline

Computer-assisted dynamic analysis has slowly but steadily won a foothold in the typical design office environment. This was primarily achieved due to the affordability of such software and the convenience of graphical user interfaces that have helped turn input data preparation and outputs presentations as routine exercises. This course introduces engineers and architects to the fundamental concepts in dynamic analysis and design that have to be well understood before a dynamic analysis is done on structures using "black-box" software tools. This course covers a discussion on the response spectra analysis and eigenvalue analysis with particular emphasis on how to interpret results from such analysis. Common pitfalls encountered in applying results from such analysis to design are discussed at length.

Learning Objective

After completing this course, the student will:

1. have a fundamental understanding of the underlying concepts in structural dynamics
2. have the required expertise to be able to carry out a computer-assisted dynamics analysis
3. have a better understanding of his/her structure through dynamic responses such as periods, modes and spectra values.
4. be able to consider accidental torsion in a dynamic analysis and be able to determine if values reported by a commercial program are good or invalid.

Course Content

1. Introduction

Most building codes suggest two ways of carrying out analysis for buildings subjected to earthquake loads, i.e., the equivalent static force procedure and a dynamic analysis procedure based on "accepted principles of dynamics". There are, of course, guidelines specified by these building codes when to use either. The equivalent static force procedure has been in use for many years now and its use is quite straightforward. However, true dynamic analysis procedures, particularly response spectra analysis, have gained foothold in the design offices only recently, mainly thanks to the proliferation of affordable and fast FE-based building analysis programs that provide both analysis procedures for users.

Here, a detailed discussion of the fundamental concepts of dynamic analysis, as implemented in most commercial structural analysis software, is provided with the objective of equipping potential users with a solid background required to use these programs sensibly. However, one should note that the time history analysis, one of the dynamic analysis procedures based on "accepted principles of dynamics", is still not ready for routine design office implementation mainly due to its massive input and output data generation and inadequately developed design guidelines and, therefore, is not included for discussion here. Nevertheless, time history analysis has traditionally been regarded by the academic community as more reliable and rational tool for dynamic analysis.

2. Basics of Dynamic Analysis

Most building codes require that a dynamic lateral force analysis procedure be used for buildings with stiffness, weight or geometric irregularity in plan or elevation. Also depending on the seismicity of the area and the height and fundamental period of the building, most codes stipulate that only a theoretically sound dynamic analysis on a three-dimensional model of the building be carried out. Response spectra analysis and time history analysis are the two most common dynamic analysis procedures available to users of commercially available building analysis programs. These two methods are well documented. A thorough familiarity with their underlying basic concepts is a requirement for any serious user of modern analysis tools used for dynamic analysis and design.

This course focuses on the response spectra analysis (RSA), as it is the method that seems to have a very significant foothold in the industry. On the other hand, while time-history analysis using a number of earthquake records provides a truly exact dynamic analysis procedure, its use in routine engineering practice is limited, as pointed out above, largely due to the massive amount of computation required. In addition, time history analysis is considered complete only after the analysis is repeated for a number of earthquake motion records; an exercise that imposes huge demands on the analyst’s time and effort budget. RSA on the other hand, provides a rational and practical approximate method based on fundamental principles of dynamics and random vibration.

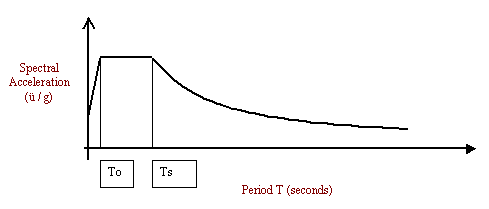
By definition, the response spectra analysis procedure involves the evaluation of the maximum value of structure responses such as displacements and member forces for each mode of vibration using a spectrum of earthquake records. These spectra values represent an estimate of the maximum possible structural response (i.e., displacements, member forces, drifts, base shear, etc) and are obtained from each of the building’s modes using one of the standard combination schemes used widely in the industry such as CQC (Complete Quadratic Combination) or SRSS (Square Root of Sum of Squares). The earthquake spectrum, on the other hand, is an average of a number of earthquake records modified for site-specific conditions and then smoothed out for design purposes. These are specified by the appropriate building code or in many cases supplied by the geotechnical engineer. A typical response spectrum curve is given in Figure 2.

A unique and often confusing aspect of RSA is that all response spectra results do not have a sign. The signs are lost during the modal combinations, which basically involve squaring modal values and taking the square roots at a later point.

Since the RSA method relies on the extraction of what are called modes and mode shapes, it is prudent to first review how such quantities are extracted and used in dynamic analysis. Eigenvalue analysis, an established mathematical procedure, is used to extract these modes and mode shapes. The following section overviews the basic concepts and procedures in eigenvalue analysis.

3. Eigenvalue Analysis – What Every Structural Dynamics Software User Needs to Know

A dynamic analysis is always preceded by what is called an eigenvalue analysis where the periods and modes of the structure are determined based on its stiffness and mass properties. Also, the static force procedures require the determination of the building period using either an approximate formula (also commonly called as Method A) or a more rigorous and theoretically sound methodology formula (also called Method B). Both methods A and B are available in most structural analysis programs. In some cases, engineers have opted to use the Ritz method (which is also classified as Method B by the code), which provides an approximate but "theoretically sound" method for getting an estimate of the building period. However, the Ritz method is still an approximate method used typically for small-scale problems and hand calculations.

The free vibration equations of equilibrium are of the form:

[K]{U} + M{} = {0}             Eq. (1)

Assuming a periodic solution to the above problem, a generalized statement commonly called "eigenproblem" or "eigenanalysis" is formulated.

[K] {} = ²[M]{}              Eq. (2)

where [K] is the building lateral stiffness matrix and [M] is the lumped diagonal mass matrix. The eigenvalue extraction (also known as eigenproblem) consists of determining the frequencies () and mode shapes () of the structure. Note that, the structural periods in the global X and Y directions could be used to evaluate generated static seismic loads.

There are a number of algorithms available for extracting the modes and mode shapes in Equation 2. The subspace iteration method [Bathe, 1987] is one such method used to extract these quantities. This is a well-tested and quite robust method, which has found wide-use in large-scale finite element programs. This method is particularly efficient for systems with large bandwidths.

 



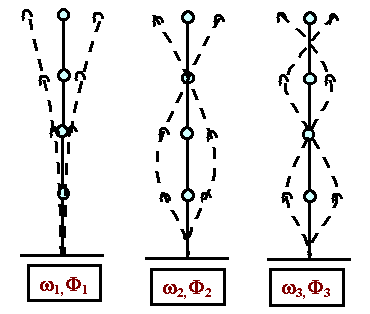
Figure 1. The First Three Mode Shapes in a 4-Lumped Mass Model

For a one degree of freedom system, Equation 2 can further be simplified to the following form:

w = √K/M             Eq. (3)

Equation (3) has an interesting and helpful significance because it establishes the relationship between stiffness and mass in dynamics. The equation suggests that the frequency of a structure is directly proportional to the stiffness but inversely proportional to the mass. Structures with large masses have low frequencies of vibration (and hence long periods); whereas structures with low masses have high frequencies of vibration (and hence short periods)..

Periods and modes obtained from an eigenvalue analysis serve as very good indicators of the behavior of the building structure under investigation. Large periods indicate a flexible structure and are common in taller buildings. Short periods are the characteristics of very rigid buildings. Most short shear wall buildings have structural periods in the range of 0.1 – 0.5 seconds. An error in eigenvalue analysis usually indicates a problem with the model of the building. Usual culprits include, lack of stiffness in one of the in-plane directions, excessive P-Delta corrections at one or more levels, or any situation where a higher stiffness is associated with a small mass or a small stiffness is associated with a huge mass.

4. Basic Review of Response Spectra Analysis

Most commercial analysis software available in today’s market provides users the ability to perform RSA for any specified earthquake input. In most case, typical response spectrum curves are provided by the program itself along with an option for users to define their own spectrum curves.

In typical analysis software, a typical response spectra analysis involves the definition of direction of interest, damping ratio, combination scheme for the modal responses and selection of earthquake record. Since mode-shapes are required for RSA, it is always preceded by an eigenvalue analysis. It is important to note that most building codes require that the eigenvalue analysis extracts enough periods and mode-shapes to generate at least 90% participation in each of the three lateral directions. Once the modes of vibrations are extracted, RSA evaluates the required response (displacement, member force, base shear, interaction equation etc.) for each mode and combines them by some statistical scheme such as the complete quadratic combination (CQC), square root of sum of squares (SRSS) or Gupta’s method. Typically, it is these combined responses that are stored in the database as outputs corresponding to the given RSA load case. The SRSS combination scheme has been used widely for many decades; however, it performs well only for 2-dimensional structures and 3-D structures with no torsional rotation. CQC, on the other hand, provides accurate combination for any general configuration and its use is recommended strongly over SRSS.

 



Figure 2. Typical Response Spectrum

5. Accidental Torsion in Dynamic analysis.

Most building codes, including UBC 97 and IBC 2000, require the consideration of accidental torsional moments caused by "an assumed displacement of the center of mass each way from its actual location by a distance equal to 5 percent of the dimension of the building perpendicular to the direction of the applied forces." These accidental torsions are required to be considered in both the equivalent static load procedure and dynamic analysis.

The code requirements for evaluating accidental torsion in the equivalent static load procedure are implemented in most building analysis tools in a straightforward manner. However, most building analysis software users are not clear on how to model accidental torsion in dynamic analysis.

There are basically two approaches allowed by most codes such as UBC 97 and IBC 200 to account for accidental torsion in dynamic analysis.

Approach 1. Move the center of mass +/- 5% in either direction. This will amount to 4 independent runs. This is exact but the major drawback is that the user needs to run the analysis four times resulting in huge output that is not easy to go through, particularly for each member.

Approach 2. This is the most practical one. The code allows running a "static" run with a torque applied at each story level to approximate accidental torsion. Users need to define 4 static seismic load cases with a load of unity magnitude applied at calculated eccentricity to produce torque. Once the analysis for the dynamic load cases plus the four "equivalent" static load cases is completed, the dynamic load cases need then to be combined with these torsion load cases.

While the direct inclusion of accidental torsion in equivalent static force procedure has been used routinely, its use in dynamic analysis, however, has not been automated by all commercial software. As a result, most engineers had relied on approximate analysis that involved, along with the dynamic load case, running a "static" case with a torque applied at each story level to approximate accidental torsion.

The hope is that more and more software will implement the direct inclusion of accidental torsion in dynamic analysis thereby allowing engineers to use this feature and save valuable time. There are, however, a number of issues users need to keep in mind in obtaining useful and accurate building behavior representation in dynamic analysis with accidental torsion.

As starters, it is always advisable to run additional regular dynamic load cases without considering eccentricity. These cases should be used as a check on the effect of eccentricity on dynamic base shears. In general, the change in centers of mass by 5% (or 10% for Canadian Codes) when doing dynamic analysis with eccentricity considered should not introduce excessive changes in base shears. However, users need to note that for non-symmetrical buildings, the base shear distribution and magnitude corresponding to dynamic load cases with eccentricity considered could be significantly different from dynamic analysis with no eccentricity. In such cases, the user has to make sure that these variations are consistent with the mass and stiffness properties of the structure under consideration.

Most codes require that at least 90% mass participation factor in each of the lateral directions be obtained for the mode-shape extraction used for dynamic analysis. Naturally, the same goes for dynamic analyses with centers of mass shifted. Therefore, it is important to make sure such participation level is achieved by running an "eigenvalue" load case and studying the mass participation factor output.

6. Orthogonal Effects in Dynamic Analysis

It is obvious that well designed buildings are expected to resist earthquake loads in all possible directions. For rectangular buildings, most codes had stipulated that members be designed for 100% of the earthquake load in a given direction plus 30% (or 40% depending on the code) of an earthquake load in the perpendicular direction.

Some commercial programs do not handle this requirement automatically. In such cases, users need to run two orthogonal dynamic load cases and manually combine them as per the code specification. However, an increasing number of structural engineering software has started implementing this feature. For an arbitrarily shaped building, a recent methodology based on what is called CQC3 algorithm has been proposed. Its popularity, however, is yet to be seen.

7. Using Results from Dynamic Analysis in Design

The response spectra analysis procedure involves the evaluation of the maximum value of structure responses such as displacements and member forces for each mode of vibration using a spectrum of earthquake records. Typically, it is these combined responses that are stored in the database as outputs corresponding to the given RSA load case.

Each response spectra case in a given direction is treated as a separate load case. Response spectra outputs have the following distinct characteristics:

• They are obtained by combining the responses from each mode of vibration by a statistical method such as CQC, SRSS or Gupta’s method to arrive at the most probable maximum values.
• Unlike outputs from static load cases, they do not have signs. The signs are lost during the modal combination.

Since RSA gives maximum possible responses without their signs, one needs to be careful in understanding the physical meaning of the quantities calculated. Strictly speaking, for example, story drift and building deflected shapes corresponding to RSA have no meaning since they represent only possible maximum value corresponding to a given earthquake record. Therefore, their use in the design process is marginal. On the other hand, RSA quantities such as base shears, overturning moments, and support reactions are useful for design purposes and could be used directly. Regarding load combinations, since displacements and member forces from response spectra analysis have no signs, load combinations involving such load cases have to include both "+" and "-" cases. For example, for the design of beams, braces, columns and foundations, strength and stability checks should be made for both tension and compression cases.

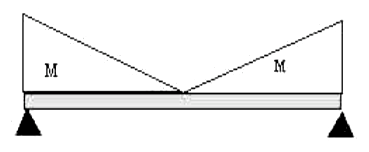
For instance, the calculation of allowable stresses in bending, i.e., Fbx and Fby in the AISC-ASD code requires the evaluation of the factor for equivalent uniform moment, Cb and the moment magnification factor Cm for certain conditions. In these expressions, both M1 and M2 (design moments at ends i and j of a segment) have signs and determine whether a member is in single or double curvature. The absence of any sign in response spectra results will give erroneous results if such expressions are used as they are since the contributions of RSA to M1 and M2 are always positive implying single curvature.

Using unsigned M1 and M2 in typical design checks for load combinations involving spectra analysis has given a value of Cb which is equal to about half of an equivalent static lateral load. This underestimation of the Cb values will result in magnifying the interaction equations in a similar amount resulting in overly conservative design values. This effect is more pronounced for members subjected to predominately bending effects, as in beams with small or no axial loads.

Figure 3. Bending Moment Diagram for a Beam under Dynamic Load

For most building structures the approximate method of working with maximum spectra values could be adopted with a fairly good accuracy.

The working stress method (ASD) is affected more by this fact since it tends to determine moment magnification factor Cmx and the equivalent moment factors Cbx and Cby as functions of moments with sign. It is suggested that for ASD, the signs of the end moments from RSA need to be recovered in accordance with a statically acceptable procedure. For beams, it is reasonable to assume that the deflections will be in double curvature under lateral earthquakes and single curvature under vertical earthquakes. For most buildings stiffened by braces and moment frames, it is also reasonable to assume that columns and braces will deform in double curvature under lateral earthquakes. The exceptions are columns in very slender and tall buildings that deform in a predominately cantilever type mode where the columns will experience single curvature. This complication might discourage the use of ASD code-checks for all types of elements.

The limit state method (LRFD) stress check algorithms, on the other hand, tend to give more reasonable interaction equations since, for most practical cases, they do not depend on the signs of the member forces. Therefore, the LRFD method is recommended when the approximate approach of design checks using maximum spectra values is used.

8. Conclusion:

This course introduces practicing engineers and architects to the fundamental concepts of structural dynamics analysis and design, which are increasingly becoming quite common in design offices thanks to the proliferation of analysis software.

Concepts of eigenvalue analysis and response spectra analysis are discussed in detail along with the implication of results from such analysis on design.

References and Further Readings

1. AISC, 1989, Manual of Steel Construction, Allowable Stress Design, 9^th Edition, AISC, Chicago, IL, 1989.
2. AISC, 1994, Manual of Steel Construction, Load and Resistant Factor Design, 9^th Edition, AISC, Chicago, IL, 1994.
3. ASCE, 1996, Minimum Design Loads for Buildings and Other Structures – ANSI/ASCE 7-95, American Society of Civil Engineers, 1996.
4. Bathe, K. J., "Finite Element Procedures in Engineering Analysis", Prentice Hall, Inc., Englewood Cliffs, New Jersey, 1982.
5. Naiem, Farzad, "The Seismic Design Handbook", Van Nostrand Reinhold, NY, 1989.
6. Reddy, J. N., "Introduction to the Finite Element Method", McGraw Hill, NY, 1987.
7. Kassegne, S.K., "FE-Based Three Dimensional Static and Dynamic Building Analysis", March 1999, A Publication of RAM International, Carlsbad, CA 92008.

 

Once you finish studying the above course content, you need to take a quiz to obtain the PDH credits.

---

DISCLAIMER: The materials contained in the online course are not intended as a representation or warranty on the part of PDHonline.com or any other person/organization named herein. The materials are for general information only. They are not a substitute for competent professional advice. Application of this information to a specific project should be reviewed by a registered professional engineer. Anyone making use of the information set forth herein does so at their own risk and assumes any and all resulting liability arising therefrom.

---