Soil Slope Stability Analysis Using the Friction Circle Method Programmed in EXCEL - An Online Course for Engineers and Architects

Soil Slope Stability Analysis Using the Friction Circle Method Programmed in EXCEL

Course Outline

1. Introduction
2. Economics and safety of excavations
3. Computer speeds calculations
4. Friction circle theory
5. Define parameters and starting point for calculations
6. Calculate the soil weight and center of gravity
7. Locate the intersection point of the cohesion and weight vectors
8. Define passive force vector
9. Resolve the static equations
10. Install in computer for a range of slip circle radii
11. Iterate the setback to find the maximum required cohesion
12. Compare to published stability numbers to ensure accuracy of computations
13. Expand program to calculate compound slopes
14. Modify program for partial height shoring
15. Summary

This course includes a multiple choice quiz at the end.

Learning Objective

The purpose of this course is to show the reader that slope stability design by friction circle theory can be easily and accurately calculated by PC computer using EXCEL worksheets. This powerful program can solve in seconds which used to take days or weeks to calculate by hand. The reader will be able to readily design both safe and economical excavation solutions. In today's competitive construction market it is crucial to be able to design the steepest possible stable temporary excavation slopes. With crew and public safety a first priority, the designer can not afford to rely on guesses and hope to be correct. OSHA offers guidelines that are so ultraconservative as to be considered impractical and the classification subject to opinion. With this program tool in hand the slope designer can instill confidence in crews, engineers, inspectors, owners and satisfy OSHA requirements.

Course Introduction

Almost all major projects require temporary construction slopes. Building foundations, pipe trenches, bridge piers and dams are common examples. Selecting the right temporary excavation slope can be critical. If it is too steep it can collapse, causing delay, extra cost and even death If the slope is too flat, unnecessary and expensive excavation and backfill will be done. There may be nearby obstructions or structures that must be protected. Will bank shoring be required or will the ground stand on a slope steep enough to eliminate or minimize the shoring?

Fortunately, over the last few years the concern for crew safety has taken first priority on the construction site. But this concern for safety has made construction slope stability a major issue of controversy. The geotechnical reports often sidestep the issue by merely citing OSHA or offering ultraconservative solutions that must be ignored. OSHA only recognizes four soil classes: Rock, Type A, Type B and Type C. OSHA will allow only rock to be cut vertically without worker protection. The designed cut slope for Type A soils is ¾ horizontally to 1 vertically. Type B soils can be cut no flatter than 1 to 1. Type C soil must be cut on at least a 1.5 to 1 slope. OSHA further make no distinction for bank heights between five and twenty feet high. In reality, other than supersaturated soils or dry cohesionless sands and gravels, nearly all native dewatered soils will safely stand temporarily on a ¾ to 1 slope up to 20 feet high. It requires a professional engineer to design the bank if it is to be cut steeper than the OSHA designation or greater than twenty feet high.

Course Content

The selection of a construction slope usually is based on opinion, not fact. The contractor wants to build the steepest safe slope and reduce cost while the engineer and owner prefer a no risk slope.. The contractor says he has been doing this for 30 years. Engineer says how do you know your experience applies to this situation? This type of argument gets us nowhere, as both sides are relying on guesswork. But there are ways to achieve factual answers and satisfy both concerns.

Often thousands of dollars and lives hinge on the bank cut slope selection. Bank slope failure are often catastrophic and without warning. I recently was commissioned to investigate at trench failure fatality. The contractor was using an adequate trench shield. For an unknown reason one of the crew left the box and entered an unprotected portion of the trench. The bank chose that place and moment to collapse. The young man left a bride and baby to suffer his passing. It was one of the most depressing times in my career to do the forensic investigation. The accident should never have happened, because every reasonable protection was in place. The young man's death cost everyone involved dearly.

Conversely, and excavation bank cut to flat will cost unnecessary time and money. Assume a square structure excavation twenty feet deep with a bottom width of 27 feet. If the bank is cut on a 1 to 1 slope versus a ¾ to 1 slope, there is 373 cubic yard of additional excavation. The cost of that excavation and backfill is typically about $15.00 per cubic yard for an added cost of $5,595.00. If the soil must be replaced with processed aggregates, then cost can be easily increased by another $20.00 per cubic yard or $7,460.00. That makes the total cost over $13,000.00 for just one excavation.

When an engineer has the tools and proper soils data, an excavation design can be completed in less than five minutes. From start of examination of the Geotechnical report to issuing a professionally stamped recommendation usually takes me less than an hour, using a specialized computer program this author wrote. That is well worth the time spent determining the steepest, but safe slope. The reason the program was written by the author is because it was discovered that a program being used by major state department of transportation is highly inaccurate when applied to the typical construction excavation situation.

Rarely is a thorough analysis of a construction excavation bank performed. The reason for this lack of analysis is that solving an accurate solution for bank stability is one of the most complex and tedious procedures in civil engineering. There is no known direct solution. The accepted methods of slices, log spiral or friction circle must assume a solution and then plot the solution and test another. This procedure is repeated until the maximum required cohesion (shear) for a given set of parameters is found. Nobody has time to do very many of these by hand. The easier methods of Rankine and Culmann that assume a flat slip plane often produce dangerously inaccurate solutions and do not lend themselves to compound slope situations.

Friction circle theory has been around for about 100 years and is probably the most accepted method of analyzing soil slope stability. The theory is deceptively simple. The soil has three basic properties that are fundamental to the analysis:

1. Moist density of the soil in pounds per cubic foot (pcf).
2. Internal Friction angle in degrees
3. Cohesion in pound per square foot (psf)

A well prepared Geotechnical report will offer all of this data. Many soils reports do not include the direct shear test that shows the Friction angle and cohesion because it is not often used by the design engineer or the contractor. It is often well worth asking for the data or even having your own direct shear tests performed.

The in situ moisture content of the soil must be added to the dry density of the soil that is shown in the Geotechnical Report for the project site. The friction angle is a measure of the particle shape. Perfectly round ball bearings will not stand in a pile. Ball bearings have a zero Internal Angle of Friction. Dry sand will form a cone when poured on a table. That is because the angular shape of the grains does not allow the particles to roll freely past each other. Sands and gravels typically have a friction angle of 30 to 35 degrees. The friction angle is also the natural angle of repose of the soil with zero cohesion. When processed gravel is stacked off a conveyor at a mine it can be seen that the pile forms a uniform cone that maintains a constant slope between 1.5 and 2 to 1. The slope of a friction angle of 30 degrees is also 1.732 to 1

Cohesion is the shear strength of soil, the glue that binds the grains together. Cohesion can stem from many sources. If water is added to the above sand sample, it can be molded in intricate shapes such as sand castles often seen at the beach. The surface tension of the water provides a weak bond between the sand grains. The moisture present in most soils provides a significant cohesion. Often a gravel bank will safely stand on a 1 to 1 cut bank for a short duration. As the bank surface dries it will ravel to a 1.5 to 1 slope. Natural minerals that have been leached into the soil, such as caliche and salts, can provide a very strong cohesion. Heat fusion and long term overburden pressure will tend to fuse the soil grains together, producing significant cohesion.

Below is the fundamental friction angle diagram. The critical failure plane is assumed to be a circle arc. The weight of the soil mass between the circle failure plane and the exterior surfaces of the bank provides the impetus for slippage along the critical circular failure plane. The soil mass is a vertical vector passing through the center of gravity of the enclosed soil mass. The slippage is resisted by the passive soil support below the critical plane and the cohesion along and tangential to the critical failure plane. The passive soil support force is always applied as a vector passing at a distance of the slip circle radius focus times the sine of the Internal Friction Angle. The cohesion is a vector placed at the center and tangential to the failure plane arc. Statics dictate that all three forces of weight, reaction and cohesion must intersect at a single common point. Note that the intersection point is not shown on the arc.

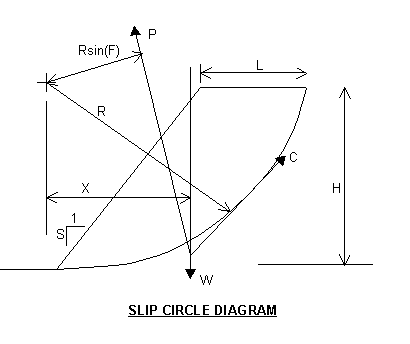
W = Soil gross weight including moisture inside the slip plane and the ground surface plus any live load surcharge.
P = The passive weight reaction.
C = The soil total cohesive resistance (shear).
R = The slip circle radius.
X = The distance from the slip circle focus to the centroid of the total weight (W).
F = The soil internal friction angle.
H = The Bank Height
L = The sip circle setback from the top of bank slope
S = The slope of the bank excavation.

Now resolve the vectors:

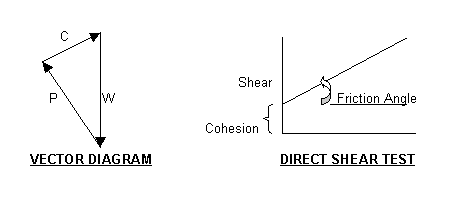
There are three statics equation available to solve the problem:

1. Conservation of the moments about the focus of the slip circle radius.

M = WX - PRsin(F) -CR = 0

2. Conservation of vertical forces:

W - Pcos(B) -Csin(D) = 0

B = the angle between the W and P vectors
D = the angel between C and the horizontal axis

3. Conservation of horizontal forces

Ccos(D)-Psin(B) = 0

The soil's internal friction angle and cohesion are found using the direct shear test. The solution to this problem becomes very complex. The slip circle radius and the set back distance are unknowns. The shape of the contained soil is complex to calculate and the centroid of the weight must be determined. Then the trigonometry of the vectors must be solved for each case of radius and setback. This is tedious and demanding for just one case. To find the critical combination of radius and setback sometimes requires hundreds of combinations to be calculated and compared. So we let the computer do the work for us.

About twenty years ago personal computers became readily available, but they lacked the power to quickly calculate a friction circle solution. Those early PCs were suitable for Rankine or Culmann theory, but those calculations can be dangerously inaccurate. Only in the last few years have PC's developed the memory capacity and speed to easily and truly solve a bank stability problem using the Friction Circle Method. Some of the programs I have seen are not designed for steep temporary construction slopes and produce highly inaccurate results.

So I started the process of writing a friction circle computer program. I selected EXCEL WINDOWS as the software base. EXCEL has all the trig functions and the equation building capability to make the calculations. EXCEL is also commonly used in the engineering and construction industries.

The first step is to define a starting point for the series of calculations. For illustration purposes we will compute a simple 3/4 to 1 slope on a 20 foot high bank. The given soil properties are a density of 100 pcf and a friction angle of 30 degrees. The radius (R) is initially defined as intersecting the toe and top of slope and the focus is exactly over the toe.

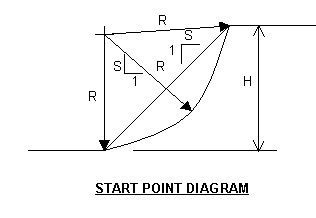
H = 20 ft
G = 100 pcf
A = 30 degrees
R = H/2 + SH/2 = 20/2 + 0.75*20/2 = 17.5 ft

The next step is calculating the mass and center of gravity.

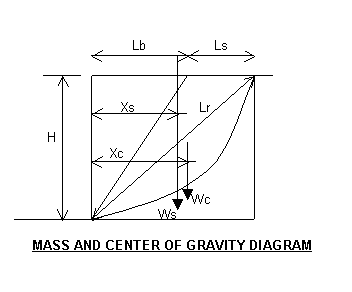
First we enclose the soil mass in a rectangle. The area of the rectangle is calculated and the triangles outside the mass are subtracted. Then the soil in the circle segment is added. The reason this technique is used, is that it makes it much easier to find the center of gravity when compound bank slopes are being analyzed.

Lb = SH = 0.75(20) = 15 ft
Ls = 5 ft

This Ls = 5 feet is an arbitrary number chosen for illustration purposes and confirmation of correct calculation as the program is developed. The setback is usually started at zero and changed until the maximum cohesion is found.

The area of the rectangle is:

Ar = H(Lb + Ls) = 20(15 + 5) = 400 sqft

The area of the soil triangle is then:

As = Ar - HLb/2 - H(Lb + Ls)/2 = 400 - 20(15)/2 - 20(15 + 5)/2 = 50 sf

The center of gravity for the soil triangle is:

Xs = [Ar(Lb + Ls)/2 - HLb^2/6 - H(Lb + Ls)^2/3]/As =
= [(50)(15 + 5)/2 - 20(15)^2/6 - 20(15 + 5)^2/3]/50 = 11.67 ft

The area of the circle segment is now calculated:
The rectangle bisecting line length is:

Lr = [H^2 +(Lb +Ls)^2]^0.5 = [(20)^2 + (15 +5)^2]^0.5 = 28.28 ft

The arcsine of one half of the circle segment is:

Bc = asin(Lr/2R) = asin(28.28/[2(17.5)] = asin(0.808) = 53.9 degrees
(EXCEL uses radians so a conversion must be made)

Lc = 4PiRBc/360 = 4(3.1416)(17.5)(53.9)/360 = 32.9 ft, is the length of the circle segment. This calculation will not be used until the cohesion calculation.

The distance from the circle center to the arc segment is:

Rb = [R^2- (Lr/2)]^0.5 = [(17.5)^2 -(28.28/2)^2]^0.5 = 10.31 ft

The area of the circle segment is:

Ac = PiBcR^2/180 - LrRb/2 = 3.1416(53.9)(17.5)^2/180 - 28.28(10.31)/2 = 142.3 sf

The centroid of the circle segment is:

Rc =5(R-Rb)/12 = 5(17.5 - 10.31)/12 = 3.0 ft

The 5/12 factor is a approximation which is accurate enough for slip circle calculations.

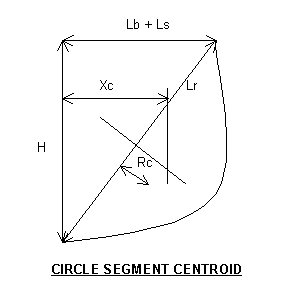
The centroid of the circle segment is

Xc = RcH/Lr + (Lb + Ls)/2 = 3(20)/28.28 + (15 + 5)/2 = 12.1 ft

The combined area of soil mass is:

At = As + Ac = 50 + 142.3 = 192.3 sf

The combined centroid of the soil mass is:

Xt = (AsXs + AcXc)/At = [(50)(11.67) + (142.3)(12.1)]/192.3 = 12.0 ft

The soil weight is:

Ws = GAt = 100(192.3) = 19,230 lbs

The next step is to locate the intersection point of forces of weight, cohesion and passive support.

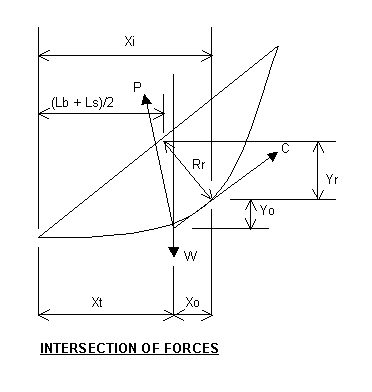
Rr = R - Rb = 17.5 - 10.31 = 7.19 ft

Xi = RrH/Lr + (Lb + Ls)/2 = (7.19)(20)/28.28 + (15 + 5)/2 = 15.08 ft

Xo = Xi - Xt = 15.08 - 12.0 = 3.08 ft

Yo = XoH/(Lb + Ls) = 3.08(20)/(15 + 5) = 3.08 ft

Yr = (Lb + Ls)Rr/Lr = (15 + 5)(7.19)/28.28 = 5.08 ft

The height of the forces intersection point above the toe of the slope is:

Yt = H/2 - Yo - Yr = 20/2 - 3.08 - 5.08 = 1.84 ft

The reason that these calculations are made will be explained later, but they are used to resolve the passive force vector.

Now as the radius and setback changes the focus of the radius will no longer be directly over the toe of the slope. This point must located horizontally in order to calculate the moment and determine the cohesion required.

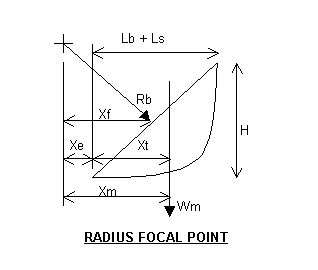
Xf = RbH/Lr = 10.31(20)/28.28 = 7.29 ft

Xe = Xf - (Lb + Lf)/2 = 7.29 - (15 + 5)/2 = -2.71 ft

Xm = Xt + Xe = 12 + (12.71) = 9.29 ft

By choosing an arbitrary set back of 5 feet, the focus of the radius is moved inside the toe vertical axis. Now the vector forces can be resolved. The below set of equations are shown to illustrate that a different approach is required to solve the cohesion using EXCEL.

The horizontal cohesion force is:

Cx = Px = Ccos(X)

Ccos(X) = (Lb + Ls)/Lr

The vertical cohesion force is:

Cy = W - Py = Csin(X)

Csin(X) = H/Lr

Py = W - Cy

C = (Cx^2 + Cy)^0.5

P = (Px^2 + Py)^0.5

M = WXm - PRsin(A) - CR = 0

WXm - {[Csin(X)^2 + (W - Ccos(X))^2]^0.5}Rsin(A) - CR = 0

WXm - {[C^2 + W^2 - 2WCcos(X)]^0.5 }Rsin(A) - CR = 0

This set of equations are difficult to reduce to directly solve for C using the EXCEL worksheet program. If the horizontal Px and Cx are canceled, a null equation is created. So the P vector has to resolved.

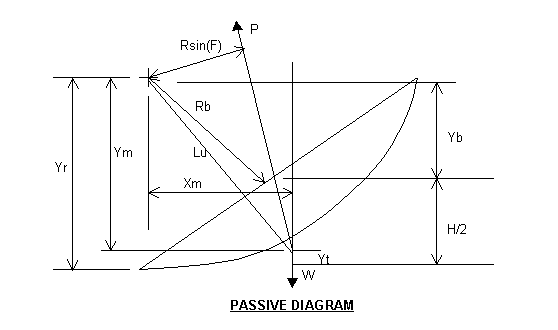
Y b = Rb(Lb + Ls)/Lr = 10.31(15 + 5)/28.28 = 7.29 ft

Yr = Yb + H/2 = 7.29 + 20/2 = 17.29 ft

Notice that Yr is less than R at 17.5 ft, that is because the focus is not directly over the toe of the slope, but the circle intersects the toe of slope.

Ym = Yr - Yt = 17.29 - 1.84 = 15.45 ft

Now the angle of the passive force can be resolved.

Lu = (Xm^2 + Ym^2)^0.5 = [(9.29)^2 + (15.45)^2]^0.5 = 18.03 ft

Fr = asin(Ym/Lu) = asin(15.45/18.03) = asin(0.8569)

Fr = 58.97 degrees

Fv = asin[Rsin(F)/Lu] = asin[(17.5)(0.5)/18.3] = asin(04781)

Fv = 29.03 degrees

Fp = 90 - Fr - Fv = 2.00 degrees

The passive force is just short of vertical (0 degrees). If the angle Fp is less than 0 degrees a negative cohesion force will be generated.

Now we can solve the equations for cohesion now that the P vector is defined.
The horizontal cohesion force is:

Cx = Px = Ccos(X)

Ccos(X) = C(Lb + Ls)/Lr = C(15 + 5)/28.28 = 0.7072(C)

Px = Psin(Fp) = Psin(2.00) = 0.0349(P)

P = Ccos(X)/sin(Fp) = (0.7072/(0.0349)(C) = 20.26(C)

Now the moment equation is:

M = WXm - PRsin(A) - CR = 0

Now subsitute the equivalent C term for P and the equation be comes:

WXm - C[cos(X)/sin(Fp)]Rsin(F) - CR = 0

Now resolve for C:

C = Wxm/{[cos(X)/sin(Fp)]Rsin(F) + R} =
= [(19,230)(9.29)]/[(20.26)(17.5)(0.5) + 17.5] = 917 lbs

The 917 pounds is the total cohesion accumulated along the circle segment.

The soil cohesion in pounds per square foot is the total cohesion divided by the circle segment length, Lc:

Cs = C/Lc = (917)/(32.9) = 27.9 psf
Because of rounding as the calculations progress, the computer will generate a slightly lower number.

As you can see this calculation is tedious at best. Not only that, but this is only one of hundreds or even thousands of radii and setbacks combinations that need to be tested to find the critical arc for a given situation. This is where EXCEL spread sheet programming comes in handy.

The first step in writing your program is to write in the bank design parameters such as height and slope with text labels above or beside the number cells. We did not address the issue here, but an equipment surcharge can be added to the soil weigh, The surcharge is usually taken as an industrial uniform load of 240 psf along Ls, with the center of gravity at Lb + Ls/2. If this is done it should be part of the parameter list. Also install an "Add to R" cell and have the original radius (R) calculation cell address the "Add to R" number cell as an add. The reason for this is in flat, high slopes, with a very low internal friction angle, the radius can be huge, many thousand feet

Now list the soil properties such as density, internal friction angle, and tested cohesion with descriptive labels beside the number cells. Also show a starting Ls, often equal to zero. The only time Lb = zero is a problem is when the bank is vertical. This places the cohesion force exactly vertical and the weight force vector and the cohesion force vector can not intersect. Now drop down a couple of rows and start installing the equations step by step in adjacent cells. Always write the equation above the equation cell so you can keep track of where you are. You can use this tutorial as a guide to make sure not mistakes are being made. Do not try to combine several steps into one long and complex equation. It will take a lot of effort to debug if you have trouble finding a mistake.

Never enter a number into the calculation cells. Always address a previous calculation cell or a previously entered parameter cell. As you go along left to right entering the calculation steps in adjacent cell, fix the address of the parameter cell that is not in the same row as the equation cell by using the F4 key or place a $ sign before the row and column designation. Once you have the solution for cohesion correctly solved, copy the entire row down one row. Now go to the original radius (R) calculation cell in the newly copied lower row and change the cell formula to read as the formula:

=1+R (actually address the cell above)

Now copy this second row down as many rows as you wish usually a hundred rows is sufficient for most construction banks. Now use a cell near the setback (Ls) number cell to install a maximum cohesion read out cell. This is done by entering: =MAX() in a cell that addresses the entire column of cohesion calculations (Cs). Now you can easily see what difference is made when you change the setback (Ls) number to find the critical combination of set back distance and radius. For each change of set back number the computer computes cohesion across a broad range of radii. The same setback (Ls) is used to calculate all radii.

Use the split screen command to make sure the maximum cohesion is within the range of radii being tested. If the cohesion calculation trend is still upward at the least radius or the maximum radius tested, then add or subtract to the radius using the "Add to R" number cell.

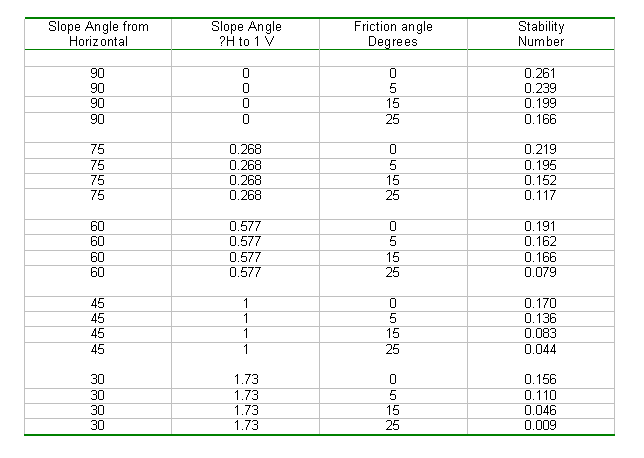
Now you have a working program. It is wise to protect the worksheet, leaving on the number entry parameter and property cells unprotected. This action will prevent accidental corruption of the program. The first step to insure the program is making correct computations. This can be established by using text book published stability numbers for simple bank slopes.

The Stability Numbers shown below are published in the text book "Soil Mechanics" by D. W. Taylor, Feb 1965.
The Stability Number is defined as: N = Cs/GH.

Cs = the required minimum cohesion for stability, psf
G = the moist soil density, pcf
H = the bank height, ft

This calculation can easily be installed and displayed as a reference. For this above calculation: N = 33/[(100)(20) = 0.0165 which a study of the below table will reveal the above calculation is not for the critical failure plane. The computer will generate the same or just slightly higher stability numbers, not more than 2%, in a couple of instances. Because the calculations were made before 1965 they were probably calculated by hand. In addition to the friction circle calculations the table also includes log spiral, slices method and Culmann theory. This represents a monumental effort and it is amazing how accurate the calculations are. By using the state of the art EXCEL worksheet software we can take the calculations to an even higher level of accuracy.

The prevailing theory at the time (pre 1970's) stated that the critical slip plane for very flat slopes and very small internal friction angles passed below the toe of the slope rather than intersecting the toe of the slope. This always puzzled me because it didn't fit common sense. By having the critical circle daylight past the toe only moved the center of mass closer to the focus of the radius of the slip circle, thereby shortening the moment lever arm length. It also increased the cohesion arc length. That only reduces the amount of cohesion required for stability. The program that the author has written shows that the critical slip circle can always intersect through the toe of the slope. This proves that only slip circles that pass through the toe of the slope need be calculated to determine the critical failure plane.

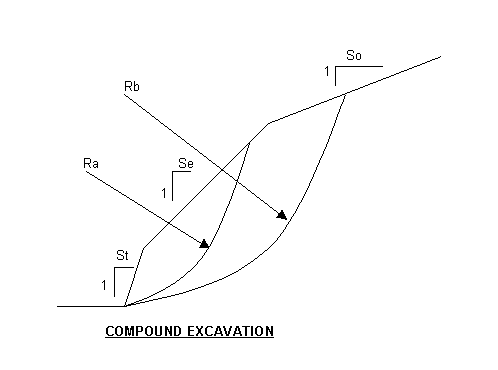
When compound slopes are being analyzed, be sure to check all possible critical slip circle configurations. In the above example either Ra or Rb can generate the critical cohesion, depending on the soil properties and excavation configuration.

The minimum recommended safety factor is 1.2 for short term exposure. This should be increased if the excavation is going to be open for a long term or there is uncertainty as to the actual soil properties. The procedure shown above assumes a dewatered condition so that the ground water table is below the critical slip circle plane.

This program can be expanded to include broken-back excavation slopes and original ground slopes. This is accomplished by introducing more triangles and rectangles that are subtracted from the slip circle enclosing rectangle. Equipment surcharges can be added by placing a uniform load along the setback length. The surcharge weight and center of gravity are added to the soil. Multiple soil layers can be analyzed where soil layers with significantly different properties will be exposed by the excavation. The upper layers are treated as triangular surcharges. Using computer lookup and macros functions the program can be almost completely automated and be very user friendly, displaying all the important data in a sketch.

The program has also been modified to generate soil pressures on shoring. This is particularly useful when only partial shoring is needed in an excavation. Most prevailing methods of calculating increased soil loadings on the shoring due to a steep overburden slope are cumbersome at best. By applying slip circle theory and using the overburden as a surcharge, an accurate active soil pressures can be accurately determined.

Course Summary

While no computer can predict unknown and unexpected soil conditions, we have become much more confident in our ability to design safe temporary construction slopes. We quickly and accurately custom design every excavation circumstance on every project. We can determine when trench shields will be effective or when positive shoring is required. We can usually determine when the soil is strong enough to be self-supporting so that speed shores are applicable. These programs have given us a powerful tool that enhances confidence and produces huge monetary savings.

The owners and engineers we work with are much more willing to accept our excavation designs, because the program reduces their uncertainty. We continue to advocate trench and excavation safety awareness because soils are variable and unexpected conditions are encountered.

References

1. Fundamentals of Soil Mechanics, Feb. 1965 by Donald W. Taylor
2. The Encyclopedia of Applied Geology, 1984 edited by Charles W. Finkl, Jr.
3. Handbook of Heavy Construction, 2nd edition, 1971 Edited by John A. Havers and Frank W. Stubbs, Jr.

Once you finish studying the above course content, you need to take a quiz to obtain the PDH credits.

DISCLAIMER: The materials contained in the online course are not intended as a representation or warranty on the part of PDHonline.com or any other person/organization named herein. The materials are for general information only. They are not a substitute for competent professional advice. Application of this information to a specific project should be reviewed by a registered professional engineer. Anyone making use of the information set forth herein does so at their own risk and assumes any and all resulting liability arising therefrom.